数据通信基础——信道特征

log₂X：2的多少次方等于X

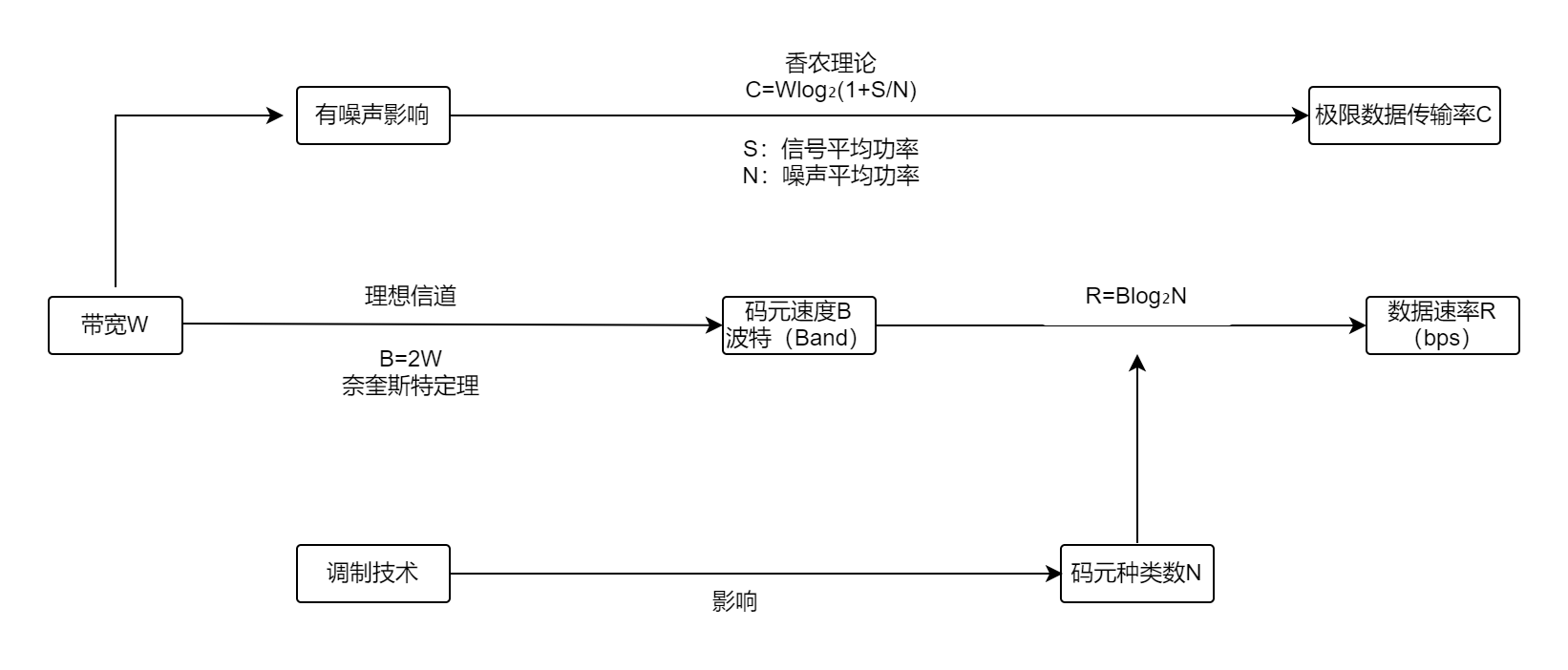
理想信道：

无噪声干扰的信道，早在1924年，奈奎斯特就推导出理想信道的码元的最高传输速率B=2W，W指信道的带宽，信号通过的信道的频率宽度，带宽=信号的最高频率-信号的最低频率，单位时赫兹（Hz）。

例如W取1Hz，在1Hz的信道情况下最高的码元传输速率时2波特（Band），也就时说每秒只能传输2个信号波形，如果每秒传输的码元超过上限，例如每秒传输3个或者4个码元，那就会造成信号波形和信号波形叠加的问题，波峰和波谷叠加就有可能导致接收到的信号波形失真严重，从而导致接收方无法判断信号里携带的信息。

奈奎斯特定理：B=2W

B:码元速度波特

W：带宽

我们在讲信道的极限传输速率的时候，不会讲它每秒多少个波特，一般讲的是每秒多个比特，波特和比特是有一个换算关系的，公式为：R=Blog₂N，R为数据速率，单位是比特，B为码元速率波特，N为码元种类数。

例如现在要传送18位的数据，111101000010101110，现在一个码元承载1位的信息量，每秒钟发送18个码元，意味着每秒钟发送18位的数据，通过公司R=Blog₂N,可以发现R=B，如果R=B，那么N就必须取2，这是对数函数，也就是说码元的种类数位2，怎么知道码元的种类数位2呢，就是用一种信号波形来表示1，用另外一种波形来表示0，所以码元种类数位2。

用一种信号波形表示1，另一种表示0，接收方就可以从信号波形中判断出发送方发了什么样一个比特信息。

现在需要想方设法提高数据传输速率，因为码元的传输速率是有上限的，那就需要用更高级的调制技术让码元种类数N变大。

例如，现在仍然传输刚刚那18位的数据，但是不是一个码元承载1位数据了，变成了一个码元承载3位数据，还是每秒钟发18个码元，那每秒钟传输的速率位54bps，因为一个码元承载3位数据，一秒钟发送18个码元，18×3=54，这里R是B的三倍，所以N等于8的。

现在是一个码元承载3位数据，所以要用不同的信号波形区分出000、001、011、111、110、100、101、010，就会有8中波形，所以N=8，也就是有8中码元总数。

噪声干扰信道

如果是有噪声干扰的信道，这时候就应该应用香浓定律。

公式：C=Wlog₂(1+S/N)

C:极限数据传输速率

W:带宽

S：信号的平均功率

N：噪声的平均功率

香农定理直接计算出极限的传输速率C

一般情况下，信号的平均功率是远大于噪声的平均功率的，会导致比值非常大，所以一般情况下描述这个比值不会直接用S/N，而是用dB，也就是分贝，S/N换算为分贝的公式为：dB=10log₁₀(S/N)。

例如，S/N=1000时，用分贝表示是30dB。

dB=10log₁₀(S/N)，现在知道S/N=1000，1000是10的3次方，再用3乘以10等于30，单位是分贝

如果带宽是3KHz，此时的极限传输数据速率就是：

C=Wlog₂(1+S/N) C=3000log₂1001 C=3000×9.97 C≈3000×10 C=30000 因为带宽1K等于1000 最后得出C=30Kbps

当分贝数是30dB时，公司可以简化为C=10W。