差错控制:
接收方收到一个信息之后,判断一个信息在传递过程中是否有误,差错控制分为检错和纠错。
检错:检查出错误但是不知道错误在什么地方。
纠错:能够检查出错误并且知道错误的是哪一位,对其进行纠正。
码距:
任何编码都是有一组码字组成,两个码之间变化的二进制位数称为码距。
换句话说,在要给编码系统中,从一个码变到另一个码所需要改变的二进制位数我们称为码距。
例如一个编码系统是由1和0组成的,现在有一组码[0,1],从0变成1,需要改变1位二进制,码距即为1。
[00,11]这个编码系统从00变成11需要改变2位,码距为2。
[0000,0011,1100,1111]这个这个的码距也为2,因为在一种编码中任意两个码之间最少变化的二进制位数称为该数据编码的最小码距。
码距与检错、纠错的关系:
1、在一个码组内为了检测e个误码,要求最小码距d应满足:d≥e+1
2、在一个码组内为了纠正t个误码,要求最小码距d应满足:d≥2t+1
例子:
A---------→B [0,1]
A为发送方,B为接收方,它们使用的编码系统是由0和1组成的,现在B收到的是一个1,请问B知不知道它收到的信息是有误的?
答案是不知道,因为它不知道A发送的是0还是1,因为1在这个编码系统中属于合法的编码方案,用公司计算:
d≥e+1,当d=1时,只有e=0时才能满足d≥e+1。
A---------→B [00,11]
现在使用两个0和两个1的编码系统,例如现在B收到的时01,很显然B已经知道收到的信息错误了,因为这套编码系统中只有00,11这两种编码方案,01时非法的,但是具体是0出错了还是1出差了B无法判断。
假设A发送的是00,B收到的是01,那么就是后面这一位出错,如果A发送的是11,B收到的是01,就是前面这一位出错,这时候套用第一个公式检错:
d≥e+1,码距为2 2≥e+1 e≤2-1 e≥1
可以检测到一个错误。
在使用第二个公式纠错:
d≥2t+1,码距为2 2≥2t+1 2t≤2-1 2t≤1 t≤1÷2 t≤0.5
错误不可能由半个错误,最后结果时t≤0,所以码距为2时只能检错,不能纠错。
A---------→B [000,111]
当使用[000,111]这套编码,码距为3,B收到的时001,编码系统里面没有这个编码方案,所以有错,通用检错公式:
d≥e+1,码距为3 3≥e+1 e≤3-1 e≤2
可以检测出两个错误
使用纠错公式:
d≥2t+1,码距为3 3≥2t+1 2t≤3-1 2t≤2 t≤2÷2 t≤1
可以对一位纠错,收到的时001,纠错1位那么只有发送方发送的时000才能纠正。
通过这个例子可以知道想要实现检错和纠错,就需要拉大码距,当码距位1,检错和纠错都不能实现,码距位2时可以实现检错不能实现纠错,码距位3时可以查出2个错误的状况,能够纠正出1位出错的状况。
奇偶校验
检错码的构造:检错码=信息字段+校验字段
奇偶校验分为奇校验和偶校验
奇校验:信息字段加上校验码字段1的个数是奇数个
偶校验:信息字段加上校验码字段1的个数是偶数个
设要传输比特信息为C1C2C3C4C5,其中校验字段C6的值“0”或“1”,经过编码以后变成六比特编码码字,其中校验码位C6应满足下列关系:
C1⊕C2⊕C3⊕C4⊕C5⊕C6=0(或1)
上述式子为模二加,所谓的模二加就是进行异或运算,两个操作数一直时结果为0,两个操作数不同时结果为1
偶校验
例如现在传输的比特信息时11011,现在需要加1位的校验位,如果用的偶校验,那么校验位应该加0,因为现在由4个1了,现在1已经是偶数了,所以不能加1了,最后要传输的校验码位110110,把校验码传输给接收方后,接收方会按照偶校验的规则进行校验,接收方会使用上面的关系是进行校验:
1⊕1⊕0⊕1⊕1⊕0 =0⊕0⊕1⊕1⊕0 =0⊕1⊕1⊕0 =1⊕1⊕0 =0⊕0 =0
最后结果是0,表示信息在传输过程中没有出错,如果结果是1则表示信息在传输过程中出现了错误。
但是具体是哪一位出错偶校验是无法确定的,因为任何一位出错都会导致模二加起来结果都是1,奇偶校验码只是做检错码,不能实现纠错功能。
它能解决奇数位出错的状况,例如出错1位,出错3位,出错5位是可以检验的,如果两位同时出错的话奇偶校验是无能为力的。
算式中的假发是模二加,上式的右边等于0称为偶校验,此时代表等式左边含偶数个1,等于1就是奇校验,含奇数个1.
海明校验
在用户信息中加入K位的校验码,加入K位的校验码就会出现2的K次方种校验信息,其中由一种表示信息在传递过程中没有出错,其他的2的K次方减1种能够指出M的位的信息和K位的这一位任意一位出错的状况。
所以海明校验中就会有M+K≤2的K次方-1这个不等式。
这就会发现你加的校验位的位数要更具用户信息它的位数来进行判断。
所谓海明校验就是把K位的校验码加入到几个奇偶校验的关系式里面去,其中有一位出错就会导致几个监督关系式它的值发送变化来定位。
例如仙子啊传递的式101101100这个信息码,请问K取几位?
首先数一下101101100这个信息码有几位,这个信息有9位,也就是M等于9,套用公式:M+K≤2的K次方-1
9+K≤2的K次方-1
最后得出的结果是4,也就是需要加入4位校验码,如果取5或者取6也可以,但是取大了会降低编码系统的效率,所以K最小取4,校验的位数是越小越好,能够满足校验需求即可。
现在知道要加入4位的校验码,这4位校验码是如何加入进去的呢,对海明校验而言,它的海明校验码一般情况下是放在2的N次方这种位置,例如2⁰、2¹、2²、2³这种位置,现在有四个校验码,分别放到2⁰、2¹、2²、2³这几个位置,也就是1、2、4、8这几个位置,所以先把这几个位置空出来。
| 数据 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
然后开始构建监督关系,因为有4个校验码,所以要有4个监督关系。
B1=B3⊕B5⊕B7⊕B9⊕B11⊕B13=1⊕0⊕1⊕0⊕1⊕0=1
B2=B3⊕B6⊕B7⊕B10⊕B11=1⊕1⊕1⊕1⊕1=1
B4=B5⊕B6⊕B7⊕B12⊕B13=0⊕1⊕1⊕0⊕0=0
B8=B9⊕B10⊕B11⊕B12⊕B13=0⊕1⊕1⊕0⊕0=0
B1监督式的构成方式是B1位置是2⁰,B3位置可以拆分成2⁰+2¹,B5位置可拆分为2⁰+2²,B7位可拆分为2⁰+2¹+2²,B9位可拆分为2⁰+2³,B11可拆分为2⁰+2¹+2³,B13可拆分为2⁰+2²+2³,总之每一位里面都包含了2⁰。
B2监督式的构成方式是B2位置是第二位,是2¹,B3可以拆分为2⁰+2¹,B6可拆分为2¹+2²,B7可拆分为2⁰+2¹+2²,B10可以拆分为2¹+2³,B11可以拆分为2⁰+2¹+2³,里面都包含有2¹。
B4和B8同理建立监督关系,计算出来的结果填入对应的位置即可得出经过差错编码的数据串:
| 数据 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
这个数据串通过网络传输到接收方,接收方在按照监督关系式进行校验:
| 数据 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
C1=B1⊕B3⊕B5⊕B7⊕B9⊕B11⊕B13=1⊕1⊕0⊕1⊕0⊕0⊕0=1
C2=B2⊕B3⊕B6⊕B7⊕B10⊕B11=1⊕1⊕1⊕1⊕1⊕0=1
C4=B4⊕B5⊕B6⊕B7⊕B12⊕B13=0⊕0⊕1⊕1⊕0⊕0=0
C8=B8⊕B9⊕B10⊕B11⊕B12⊕B13=0⊕0⊕1⊕0⊕0⊕0=1
如果接收到的数据没有错误的话,每个监督式最后计算的结果都应该等于0,但是现在只有C4等于0,其他都为1,也就式只有C4这个监督关系接收的是正确的数据,其他接收到的数据都是有错误的,既然可以同时导致3个监督关系出现错误,就说明了出现错误的这个数同时存在于三个监督关系式中,对比一下这三个监督关系式,只有B11是同时出现在出现错误的三个监督关系式中的,也就是说明B11位的数据接收错误了,只需要对B11进行纠正,如果B11的值是0则纠正为1,如果B11的值是1则纠正为0。
海明校验码是可以实现检错和纠正1位出错的。
CRC校验:
因为海明校验较为复杂,在计算机网络中一般采用CRC校验,CRC的校验方式也是用户信息加上校验字段来构成差错编码。
例如现在用户要传递的原始报文是11001010101,其生成多项式:X⁴+X³+X+1,在CRC校验中有一个概念叫生成多项式,生成多项式是收发双方约定的一个式子,这是计算CRC校验码的一个关键点。
注意:生成多项式的最高幂次方决定CRC的位数,以这个例子为例,生成多项式的最高幂次方是4,所以CRC校验码的位数是4位,具体这4位是什么就需要通过一下方程式进行计算:

首先在源码报文后添加4个0,目的是为了能够计算出真正的CRC校验码,然后把生成多项式X⁴+X³+X+1转为二进制数表示形式,转换方式为当X存在幂次方的时候为1,不存在的时候为0,有X⁴写一个1,有X³写一个1,没有X²写0,X=X¹,所以是有幂次方的,写1,1=X⁰,也写1,任何数的0次方都为1。
最后转换下来的结果是:11011
在使用模二除计算,模二除的规则为不产生进位也不会产生借位,逐位进行相减,也就是异或运算。前面为0则省略不写。

算出的结果为10,再从后面不上了3位继续运算

算出来的结果位1001
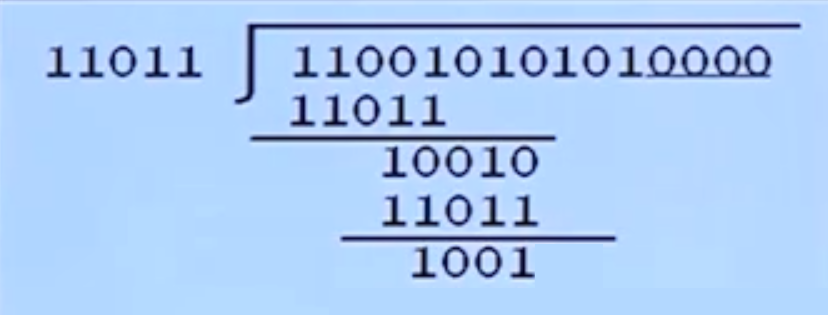
以此类推,直到算到最后面,如没有4位则在前面补0,之所以是4位是因为CRC校验码在最开始就知道了是4位,最后得出来的这4位就是CRC校验码。
最后把0011添加到原始报文后面即可得出110010101010011为经过编码后的报文。
当把数据传输到接收方,接收方收到信息后会用收到的信息除以生成多项式的二进制表现式看结果是否为0,如过结果为0则说明在传输过程中没有出错,如果在传递过程中出错都会导致结果不为0,CRC校验码一般只用做检错码,不会进行纠错,当发现错误时会要求发送方重发,而本身不会对其进行纠错。
CRC校验码在信息网络中有非常广泛的应用,例如以太网802.3这个标准,会学习到以太帧它的帧格式,帧格式当中有一个32位的CRC校验码(CRC32)。
| 网络协议 | CRC位 | 应用点 |
|---|---|---|
| HDLC | CRC16/CRC32 | 除帧标志位外的全帧 |
| FR(帧中继) | CRC16 | 除帧标志位外的全帧 |
| ATM | CRC18 | 帧头校验 |
| 以太网(802.3) | CRC32 | 帧头(不含前导和帧起始符) |
| 令牌总线(802.4) | CRC32 | 帧头(不含前导和帧起始符 |
| 令牌环(802.5) | CRC32 | 帧头(从帧控制字段到LLC) |
| FDDI | CRC32 | 帧头(从帧控制字估到INF0) |
